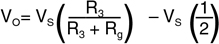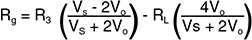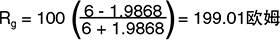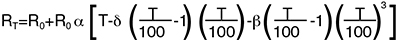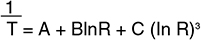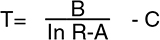|
| |
 |
 |
 |
 |
 |
□ 自供电
□ 简单
□ 耐用
□ 实惠
□ 多样
□ 温度范围广
|
□ 最稳定
□ 最精确
□ 比热电偶更线性化
|
□ 输出高
□ 快速
□ 双线电阻值测量
|
□ 最线性化
□ 输出最高
□ 实惠
|
 |
□ 非线性化
□ 电压低
□ 需要基准
□ 最不稳定
□ 最不敏感
|
□ 昂贵
□ 需要电流源
□ 磁阻小
□ 绝对电阻低
|
□ 非线性化
□ 受限的温度范围
□ 脆弱
□ 需要电流源
□ 自动加热
|
□ T<200˚C
□ 需要电源
□ 低
□ 自动加热
□ 受限的配置
□ 自动加热
|
目录
应用说明-实用温度测量 |
图1 |
-
页码
-
26
-
27
-
28
-
34
-
40
-
43
-
44
-
44
-
45
-
46
-
47
合成燃料研究、太阳能转换和新发动机开发是应对我 们日益减少的自然资源状态仅有的少数几个迅速发展的 学科。随着所有行业把新重点放在能效上,基本的温度 测量呈现出更高的重要性。本应用说明的目的是探索更 常见的温度监测技术并介绍提高其精度的过程。
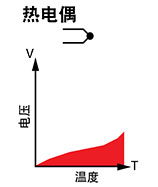
我们将重点介绍以下四种最常见的温度传感器:热电 偶、RTD、热敏电阻和集成电路传感器。尽管热电偶已 得到广泛应用,但却常被误用。因此,我们将主要集中 介绍热电偶测量技术。
附录A包含了热电偶的经验定律,这是本文中使用的 所有推导结论的基础所在。如果读者想要更深入地讨论 热电偶理论,请阅读参考文献中的参考资料17。
对于使用特定热电偶应用的人员,附录B可帮助他们 选择最佳类型的热电偶。
在本应用说明中,我们将重点强调传感器布置、信号 调节和仪器的实用考虑因素。
早期测量设备 - 伽利略在约1592年前后发明了温度 计。1, 2, 3他在开口的容器中装满有色酒精,并悬挂一个喉 部狭长的玻璃管,管顶部是一个空心球。加热后,球体 中的空气膨胀并通过液体冒出气泡。冷却球体会导致液 体在管中向上移动。1然后,可通过标注液体在管内的位 置观察球体的温度波动。这一“倒置”的温度计只是一 个简劣的指示器,因为液位会随大气压力变化并且玻璃 管没有刻度。随着佛罗伦萨温度计的发展,纳入了密封
结构和刻度尺,温度测量的精度有了巨大提高。
在随后的几十年里,人们构思了许多种温标,所有这 些都基于两个或更多固定点。但其中一种温标直到18世
纪早期才得到公认,当时荷兰的仪器制造商华伦海特 制作出了精确并且可重复的水银温度计。对于华氏温 标的低端固定点,华伦使用了冰水和盐(或氯化铵) 的混合物。这是他能够重现的最低温度,并且他将其 标记为“零度”。对于华氏温标的高端,他选择了人 体血液温度并将其标为96度。
为什么是96度而不是100度?这是因为早期的刻度 被分成十二等份。而华伦显然为了努力追求更高的分 辨率,而将华氏温标分成24等份、48等份乃至最终的
96等份。
华氏温标得到普及主要是因为华氏制造温度计的可 重复性和质量。
约1742年,安德斯摄尔修斯提出将冰的融点和水的 沸点用作温标的两个基准。摄尔修斯选择将零度作为 沸点而将100度作为融点。后来,这两个端点被颠倒过 来,百分度温标就这样诞生了。1948年,该温标正式 更名为摄氏温标。
19世纪早期,威廉汤姆森(开尔文男爵)根据理想 气体的膨胀系数制定了通用的热力学温标。开尔文确 立了绝对零度的概念,开氏温标仍然是现代温度测量 的标准。
四种现代温标的转换公式如下:
˚C = 5/9 (˚F - 32) ˚F= 9/5 ˚C + 32
K = ˚C + 273.15 ˚R= ˚F + 459.67
兰金温标(˚R)仅仅是开氏温标的等效温标,以热力学 领域早期的先驱W.J.M.兰金的名字命名。
我们可以建立电压分配器而无法建立分温器,我们不 能像以增加长度来测量距离那样增加温度。我们必须依 赖通过物理现象确定的温度,这些温度易于观察且本质 不变。国际实用温标(IPTS)就是基于此类现象。1968年 修订版确定了十一项基准温度。
由于这些固定的温度只能用作基准,因此我们必须使 用仪器在这些温度之间插补。但在这些温度之间精确插 补可能需要一些相当特异的传感器,其中许多传感器太 过复杂或昂贵而无法在实际情况中使用。我们将只讨论 以下四种最常见的温度传感器:热电偶、电阻式温度检 测器(RTD)、热敏电阻和集成电路传感器。
平衡点 |
K |
0C |
| 氢的三相点 |
13.81 |
-259.34 |
| 氢的液相/气相 |
17.042 |
-256.108 |
| 在25/76标准 大气环境中 |
| 氢的沸点 |
20.28 |
-252.87 |
| 氖的沸点 |
27.102 |
-246.048 |
| 氧的三相点 |
54.361 |
-218.789 |
| 氧的沸点 |
90.188 |
-182.962 |
| 水的三相点 |
273.16 |
0.01 |
| 水的沸点 |
373.15 |
100 |
| 锌的冰点 |
692.73 |
419.58 |
| 银的冰点 |
1235.08 |
961.93 |
| 金的冰点 |
1337.58 |
1064.43 |
| 点 |
表1 |
|
当由不同金属组成的两根电线两端项链并且对其中一 端进行加热时,热电电路中会有连续的电流流动。托马 斯塞贝克在1821年发现了这一现象。
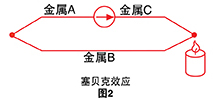
如果此电路在中央断开,则净开路电压(塞贝克电 压)是连接点温度和两种金属成分的函数。

所有不同的金属都展示出这种效应。两种金属的最常 见组合如该应用说明的附录B所示,并且列出了它们的 重要特性。对于小的温度变化,塞贝克电压与温度成线 性比例。
ΔeAB = αΔT
其中塞贝克系数α是比例常数。
测量热电偶电压–我们无法直接测量塞贝克电压,因为 我们必须首先将电压表连接到热电偶,然后电压表会自 己创建一个新的热电电路。
让我们将电压表跨接到铜-康铜(T型)热电偶并查看 电压输出:
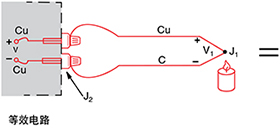
等效电路
 使用DVM测量连接点电压 图4
使用DVM测量连接点电压 图4
我们希望电压表只读V1,但我们已通过连接电压表尝 试测量连接点J1的输出,创建了两个更具金属性的连接 点:J2和J3。由于J3是铜-铜连接点,因此它不会建立热 电动势(V3 = 0),但J2是铜-康铜连接点,将会添加一个相 对于V1的电动势(V2)。产生的电压表读数V将与J1和J2间 温差成正比。这就是说,我们只有在确定J2的温度之后 才能确定J1处的温度。
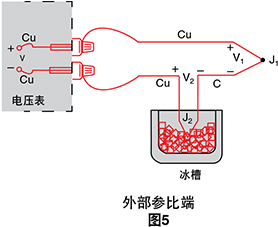
确定J2温度的方式之一是以物理方式将连接点放入冰 槽中,强制使其温度成为0˚C并确定J2作为参比端。由于 两个电压表端子连接点现在为铜-铜,因此不会产生热电 动势并且电压表上的读数V与J1和J2间的温差成正比。
现在,电压表读数为(见图5):
V = (V1 - V2) ≅ α(tJ1 tJ2)
如果我们以摄氏度指定TJ1,则:
TJ1 (˚C) + 273.15 = tJ1
则V变为:
V = V1 - V2 = α [(TJ1 + 273.15) - (TJ2 + 273.15)]
= (TJ1 - TJ2) = (TJ1 - 0)
V = TJ1
我们使用这一延伸的推导重点强调冰槽连接点的输出 V2并非零伏。它是绝对温度的函数。
通过添加冰点参比端的电压,我们现在将读数V参照 0˚C。由于冰点温度可以精确控制,因此该方法非常精 确。(美国)国家标准局(NBS)使用冰点作为其热电偶 表的基本基准点,因此我们现在可以查看NBS表并直接 从电压V转换为温度TJ1。

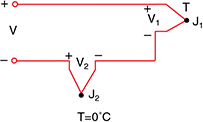
图5所示的铜-康铜热电偶是一个独特的示例,因为 铜线和电压表端子使用的是相同的金属。让我们使用
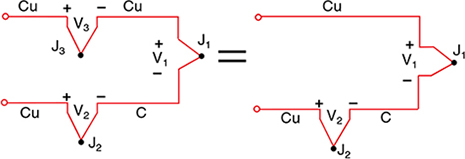
铁-康铜(J型)热电偶取代铜-康铜热电偶。铁线(图6) 增加了电路中不同金属连接点的数量,因为两个电压表 端子都变成了Cu-Fe热电偶连接点。
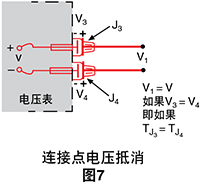
如果两个前面板端子温度不同,将会出现错误。要进 行更精确的测量,应延长电压表铜导线以便铜-铁连接点 位于等温(相同温度)块上:偶连接点。
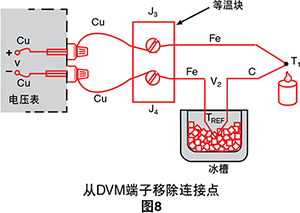
等温块是电绝缘体,但确实是良好的热导体,它用于 使J3和J4保持相同的温度。绝对块温度并不重要,因为 两个Cu-Fe连接点的作用是相反的。我们仍得到如下结果
V = α (T1 - TREF)
让我们将冰槽替换成其他等温块
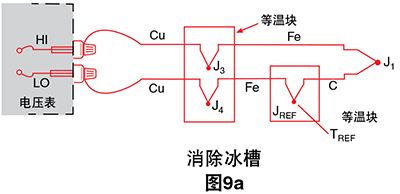
新块处于基准温度TREF,并且由于J3和J4仍处于相同温 度,我们可以再次显示
V = α (T1-TREF)
这仍然是一个非常不方便的电路,因为我们必须连接 两个热电偶。让我们将Cu-Fe连接点(J4)和Fe-C连接点(JREF)合并,消除负极(LO)导线中多余的Fe线。
我们可以通过首次连接两个恒温快(图9b)来实现这 项操作。
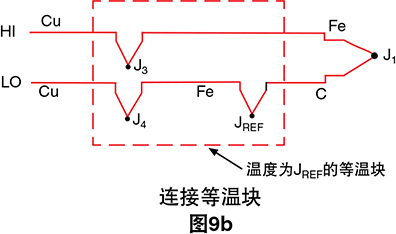
我们没有更改输出电压V。它仍然是
V = α (TJ1 - TJREF )
现在,我们将调用中间金属定律(请参阅附录A)来 消除额外的连接点。这一经验“定律”表明,在热电偶 连接点的两种不同金属之间插入第三种金属将不会影响 输出电压,只要附加的金属形成的两个连接点处于相同 的温度:

因此,图9B中的低电平导线: 变为:
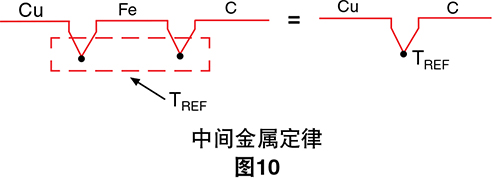
这是一个非常有用的结论,因为它完全消除了LO导线 中对铁线(Fe)的需要:
 同样,V = α (TJ1 - TREF),其中α是Fe-
同样,V = α (TJ1 - TREF),其中α是Fe-
C热电偶的塞贝 克系数。
连接点J3和J4代替冰槽。这两个连接点现在成为 参比端。
现在,我们可以继续下一逻辑步骤:直接测量等温块(参比端)的温度并使用该信息计算未知温度TJ1
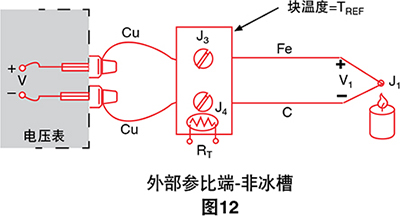
热敏电阻(其电阻RT是温度的函数)为我们提供了测 量参比端绝对温度的一种方式。由于等温块的设计,连 接点J3和J4以及热敏电阻全部假设为相同温度。通过计 算机控制的数字万用表,我们只需:
- 测量RT以确定TREF,然后将TREF转换为其等效 参比端电压VREF
- 测量V后加上VREF得出V1,然后将V1转换为温 度TJ1。
此过程称为软件补偿,因为它依靠计算机软件来补偿 参比端的影响。该等温接线盒温度传感器可以是具有与 绝对温度成正比特性的任何设备:RTD、热敏电阻或集 成电路传感器。
询问以下问题似乎符合逻辑:如果我们已经拥有测量 绝对温度的设备(如RTD或热敏电阻),为什么我们要 自寻麻烦而使用需要参比端的热电偶?此问题最重要的 唯一答案是热敏电阻、RTD和集成电路传感器仅在特定 的温度范围内有用。另一方面来说,热电偶可用于广泛 的温度范围,并且已针对各种大气环境进行了优化。它 们比热敏电阻耐用得多,事实证明,热电偶通常焊接到 金属部件或用螺钉夹紧。它们可以通过钎焊或焊接现场 制造。简言之,热电偶是现有的使用最广泛的温度传感 器,由于测量系统执行参比端补偿和软件电压到温度转 换的整个任务,因此使用热电偶变得与连接一对电线一 样容易。
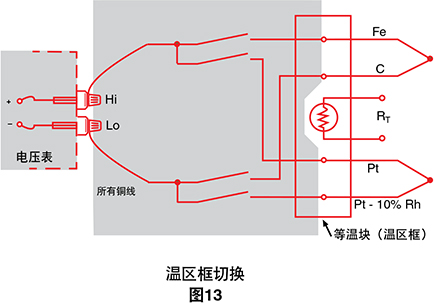
当我们需要监测大量数据点时,热电偶测量变得尤其 方便。这通过对多个热电偶元件使用等温参比端来实现(见图13)。
舌簧继电器扫描器可将电压表按顺序连接到各种热电 偶。无论选择何种类型的热电偶类型,所有电压表和扫 描器导线都是铜的。事实上,只要知道每个热电偶是什 么,我们就可以在同一等温接线盒(通常称为温区框) 中混合使用各种类型的热电偶,并在软件中进行相应的 修改。接线盒温度传感器RT位于盒中心,从而将由于热 梯度导致的误差减至最低。
软件补偿是用于测量热电偶使用最广泛的技术。许多 热电偶都在相同的块上连接,铜导线在整个扫描器内使 用,并且该技术与所选的热电偶类型无关。此外,当数 据采集系统与内置的温区框配合使用时,我们只需如同 连接一对测试引线一样连接热电偶即可。所有转换都通 过计算机执行。此技术的一个缺点是计算机需要少量额 外的时间来计算参比端温度。为获得最大速度,我们可 以使用硬件补偿。
与软件补偿的测量参比端温度和计算其等效电压不同 的是,我们可以插入一块电池抵消参比端偏移电压。此 硬件补偿电压和参比端电压的组合等于0˚C连接点的 电压。
补偿电压e 是温度传感电阻RT的函数。电压V现在参照 0˚C,可直接读取,并可以使用NBS表转换成温度。
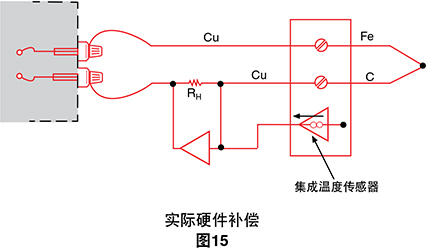
此电路的另一个名称是电子冰点基准。6 这些电路可 与任何电压表以及各种热电偶配合使用。此技术的主要 缺点是每种单独的热电偶类型通常需要唯一的冰点基准 电路。
图15显示了可与舌簧继电器扫描器配合使用以补偿整 块热电偶输入的实际冰点基准电路。块中的所有热电偶 必须为相同类型,但每块的输入可适配不同的热电偶类 型,只需更改增益电阻即可。


硬件补偿电路或电子冰点基准的优点是无需计算基准温 度。这为我们节省了两个计算步骤并使硬件补偿温度测 量比软件补偿测量更快一些。
| 硬件补偿 |
软件补偿 |
快速,
限制为每个卡一种热电偶类型 |
需要更多计算机操纵时间,
通用 - 接受任何热电偶 |
表2 |
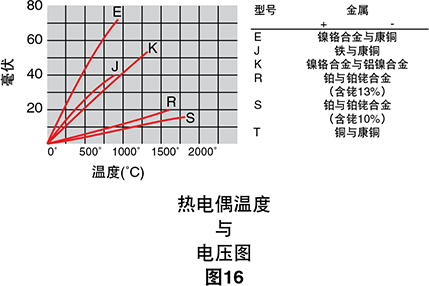
我们已使用硬件和软件补偿来合成冰点基准。现在,我们只需读取数字电压表并将电压读数转换成温度即 可。遗憾的是,热电偶的温度与电压关系不是线性的。 更常见的热电偶输出电压被绘制为图16中温度的函数。 如果绘制的曲线斜率(塞贝克系数)与温度如图17中 所示,则很明显热电偶是非线性设备。
图17中的水平线将表示常数α,换句话说,即线性设
备。我们注意到,K型热电偶的斜率在从0˚C到1000˚C 的温度范围内接近常数。因此,K型可与倍增电压表和 外部冰点基准配合使用以获得适当精度的直接温度读 数。即温度显示仅涉及一个标度因子。 此过程与电压表配合使用。
通过检查塞贝克系数的变化,我们可以很容易地看 到,使用一个恒定的标度因子将限制系统的温度范围并 限制系统精度。通过读取电压表并查阅本手册第172页 上的(美国)国家标准局热电偶表4可以得到更好的转换 精度-见表3。
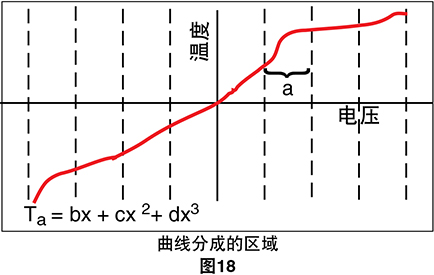
T = a0 +a1 x + a2x2 + a3x3 . . . +anxn
其中
T = 温度
x = 热电偶电动势(以伏特为单位)
a = 每个热电偶唯一的多项式系数
n = 多项式的最大阶数
随着n的增加,多项式的精度也会提高。代表性数字为 可实现± 1˚C精度的n = 9。可在较窄的温度范围内使用 较低阶数的多项式以获得更高的系统速度。
表4是用于将电压转换成温度的多项式示例。数据可打 包供数据采集系统利用。计算机不会直接计算指数,而 是编程为使用嵌套的多项式形式以节省执行时间。快速 拟合的多项式在表4中所示的温度范围以外会降级,因此 不应在这些限制范围之外推算。
| mV |
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
.10 |
mV |
| 温度单位为摄氏度(IPTS 1968) |
| 0 |
0 |
0.17 |
0.34 |
0.51 |
0.68 |
0.85 |
1.02 |
1.19 |
1.36 |
1.53 |
1.7 |
0 |
| 0.10 |
1.70 |
1.87 |
2.04 |
2.21 |
2.38 |
2.55 |
2.72 |
2.89 |
3.06 |
3.23 |
3.40 |
0.10 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 0.30 |
5.09 |
5.26 |
5.43 |
5.60 |
5.77 |
5.94 |
6.11 |
6.27 |
6.44 |
6.61 |
6.78 |
0.30 |
| 0.40 |
6.78 |
6.95 |
7.12 |
7.29 |
7.46 |
7.62 |
7.79 |
7.96 |
8.13 |
8.30 |
8.47 |
0.40 |
| 0.50 |
8.47 |
8.63 |
8.80 |
8.97 |
9.14 |
9.31 |
9.47 |
9.64 |
9.81 |
9.98 |
10.15 |
0.50 |
| 0.60 |
10.15 |
10.31 |
10.48 |
10.65 |
10.82 |
10.98 |
11.15 |
11.32 |
11.49 |
11.65 |
11.82 |
0.60 |
| 0.70 |
11.82 |
11.99 |
12.16 |
12.32 |
12.49 |
12.66 |
12.83 |
12.99 |
13.16 |
13.33 |
13.49 |
0.70 |
| 0.80 |
13.49 |
13.66 |
13.83 |
13.99 |
14.16 |
14.33 |
14.49 |
14.66 |
14.83 |
14.99 |
15.16 |
0.80 |
| 0.90 |
15.16 |
15.33 |
15.49 |
15.66 |
15.83 |
15.99 |
16.16 |
16.33 |
16.49 |
16.66 |
16.83 |
0.90 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 1.10 |
18.48 |
18.65 |
18.82 |
18.98 |
19.15 |
19.31 |
19.48 |
19.64 |
19.81 |
19.97 |
20.14 |
1.10 |
| 1.20 |
20.14 |
20.31 |
20.47 |
20.64 |
20.80 |
20.97 |
21.13 |
21.30 |
21.46 |
21.63 |
21.79 |
1.20 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 1.40 |
23.44 |
23.60 |
23.77 |
23.93 |
24.10 |
24.26 |
24.42 |
24.59 |
24.75 |
24.92 |
25.08 |
1.40 |
| |
E型 |
J型 |
K型 |
R型 |
S型 |
T型 |
| |
含镍10% 铬(+) 与 康铜(-) |
铁(+) 与 康铜(-) |
含镍10%的镍铬合金(+) 与 含镍l-5%(-) 铝硅合金) |
含铑13%的铂铑合金(+) 与 铂(-) |
含铑10%的铂铑合金(+) 与 铂(-) |
铜(+) 与 康铜(-) |
|
-100˚C ~ 1000˚C ± 0.5˚C 9阶 |
0˚C ~ 760˚C ± 0.1˚C 5阶 |
0˚C ~ 1370˚C ± 0.7˚C 8阶 |
0˚C ~ 1000˚C ± 0.5˚C 8阶 |
0˚C ~ 1750˚C ± 1˚C 9阶 |
-160˚C ~ 400˚C ±0.5˚C 7阶 |
| a0 |
0.104967248 |
-0.048868252 |
0.226584602 |
0.263632917 |
0.927763167 |
0.100860910 |
| a1 |
17189.45282 |
19873.14503 |
24152.10900 |
179075.491 |
169526.5150 |
25727.94369 |
| a2 |
-282639. 0850 |
-218614.5353 |
67233.4248 |
-48840341.37 |
-31568363.94 |
-767345.8295 |
| a3 |
12695339.5 |
11569199.78 |
2210340.682 |
1.90002E + 10 |
8990730663 |
78025595.81 |
| a4 |
-448703084.6 |
-264917531.4 |
-860963914.9 |
-4.82704E + 12 |
-1.63565E + 12 |
-9247486589 |
| a5 |
1.10866E + 10 |
2018441314 |
4.83506E + 10 |
7.62091E + 14 |
1.88027E + 14 |
6.97688E + 11 |
| a6 |
-1. 76807E + 11 |
|
-1. 18452E + 12 |
-7.20026E + 16 |
-1.37241E + 16 |
-2.66192E + 13 |
| a7 |
1.71842E + 12 |
|
1.38690E + 13 |
3.71496E + 18 |
6.17501E + 17 |
3.94078E + 14 |
| a8 |
-9.19278E + 12 |
|
-6.33708E + 13 |
-8.03104E + 19 |
-1.56105E + 19 |
|
| a9 |
2.06132E + 13 |
|
|
|
1.69535E + 20 |
|
温度转换公式: T = a0 +a1 x + a2x2 + . . . +anxn
嵌套多项式形式: T = a0 + x(a1 + x(a2 + x (a3 + x(a4 + a5x)))) (5th order)
其中x以伏特为单位,T以˚C为单位
NBS多项式系数
表4
高项式的计算对计算机来说是一项费时的任务。正 如我们之前提到的,我们可以为较小的温度范围使用低 次多项式来节省时间。在用于一个数据采集系统的软件 中,热电偶特性曲线分为八个区域,每个区域通过三次 多项式做近似处理。*
所有上述过程都假设热电偶电压可以精确轻松地进行测 量;但快速浏览表3可以看到,热电偶输出电压实际上 非常小。检查系统电压表的要求:
| 热电偶型号 |
|
塞贝克系数
(μV/˚C) @ 20˚C |
DVM灵敏度(0.1˚C) (μV) |
| E |
|
62 |
6.2 |
| J |
|
51 |
5.1 |
| K |
|
40 |
4.0 |
| R |
|
7 |
0.7 |
| S |
|
7 |
0.7 |
| T |
|
40 |
4.0 |
所需的DVM灵敏度
表5 |
即使对于常见的K型热电偶,电压表也必须能够分辨 4 μV才能检测到0. 1˚C的变化。此信号的量值是噪声潜 入任何系统的开放入口。因此,仪器设计人员可利用多 项基本的噪声抑制技术,包括树形开关、常模过滤、积 分和保护。
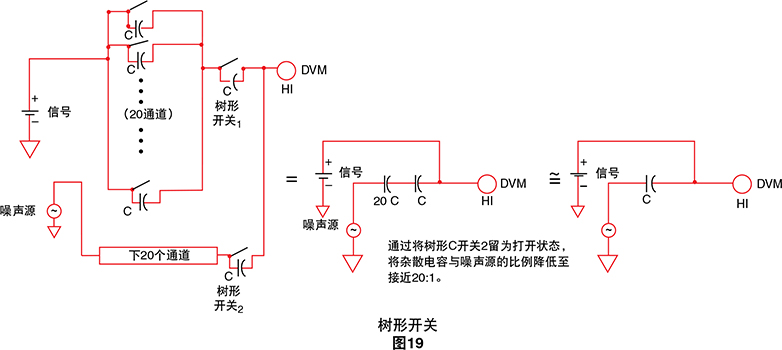
树形开关-树形开关是一种将扫描器通道分组整理的方 法,每组具有其自己的主开关。
如果没有树形开关,每个通道可以直接通过其杂散电 容发出噪声。通过树形开关,成组的并行通道电容在一 个树形开关电容中串联。由于降低了通道间电容,结果 大大减少了大型数据采集系统中的串扰。
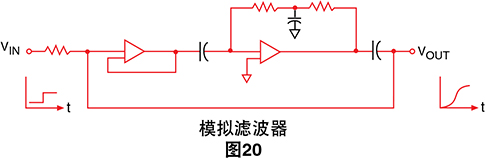
模拟滤波器-可在电压表输入端直接使用滤波器以减少 噪声。这将显著减少干扰,但会导致电压表对阶跃输入 的响应更加缓慢。
积分-积分是一项模数转换技术,从根本上均化整个线 路周期的噪声;因此供电线路相关的噪声及其谐波几乎 可以消除。如果选择的积分时间段小于积分线路周期, 则其噪声抑制属性会从根本上失效。
由于热电偶电路覆盖的长距离特别容易产生供电线路 相关的噪声,因此建议使用积分模拟到数字转换器来测 量热电偶电压。根据允许整个周期积分读取速率为每秒
48个样品的最近创新,积分是一项特别有吸引力的模数 转换技术。
保护-保护是用于从高低测量导线常见的任何噪声源M
(即从共模噪声源)减少干扰的一项技术。
我们假设热电偶线穿过的线管与220 Vac电源线相同。 电源线和热电偶线之间的电容将产生约等于两根热电偶 线上量值的交流信息。此共模信号在理想电路中不成问 题,但电压表并非理想电路。电压表的低端子和安全接 地(壳体)之间有一些电容。电流会流经此电容并流经 热电偶导线电阻,从而产生常模噪声信号。保护装置( 物理上是包围整个电压表电路的浮动金属盒)将连接到 包裹热电偶线的屏蔽装置,并用于分流干扰电流。

每个屏蔽的热电偶连接点都可以直接接触干扰源而没 有任何不良影响,因为扫描器上已进行布置,以针对每 个热电偶通道单独切换保护端子。将屏蔽装置连接到保 护装置的这一方法用于消除接地回路(通常在屏蔽装置 接地时产生)。
dvm保护装置对于消除热电偶连接点与共模噪声源直 接接触时产生的噪声电压特别有用。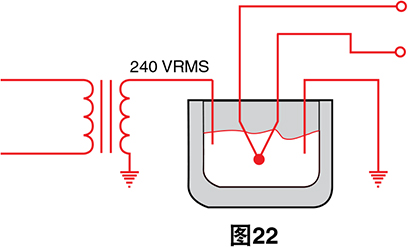
在图22中,我们想要测量正由电流加热的金属液槽 中央的温度。槽中央的电势是120 V RMS。等效电路 如下: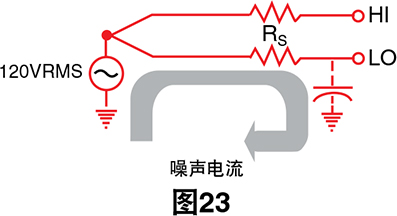
从dvm Lo端子到壳体的杂散电容会造成一个电流流经低 电平导线,这反过来会导致热电偶Rs的串联电阻间的噪 声电压下降。这个电压直接出现在dvm Hi到Lo端子间, 并导致噪声测量。如果我们使用保护导线直接连接到热 电偶,则会明显减少Lo导线中的电流。现在,噪声电流 流经不影响读数的保护导线: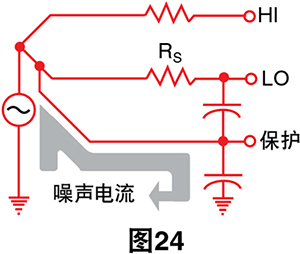
请注意,我们也可以通过最大限度减小Rs来最大限度 减小噪音。我们使用线径更大的热电偶线(串行电阻更 小)来实现这项操作。
为了减少发生磁感应噪声的可能性,热电偶应以统一 的方式绞合。市场上可以买到的热电偶延长线都是双绞 线配置。
实用的预防措施-我们讨论了参照端的概念、如何使用 多项式提取绝对温度数据,以及要在数据采集系统中寻 找的内容来最大限度降低噪音的影响。现在,让我们来 了解一下热电偶线本身。多项式曲线拟合依赖于完善的 热电偶线;也就是说在执行温度测量期间,热电偶线必 须不能被失准。现在我们将讨论热电偶温度测量的一些 误区。
除数据采集系统及其温区框的指定精度以外,大多数 测量误差可以追溯到以下主要来源之一:
- 不良连接点连接
- 热电偶线的失准
- 分流阻抗和电蚀作用
- 热分流
- 噪声和泄漏电流
- 热电偶规格
- 记录文档
连接两根热电偶线有许多可接受的方法:钎焊、银钎 焊、焊接等。热电偶线钎焊在一起后,我们可在热电偶 电路中插入第三种金属,只要热电偶两端的温度相同, 焊料应不会引起任何错误。焊料不会限制此连接点可承 受的最高温度。要达到较高的测量温度,必须焊接接 头。但焊接并非一个可以轻率进行的过程。5过热可能会 降低电线的性能,并且焊接电线的焊接气体和空气都可 能会扩散到热电偶金属中,从而更改其特性。困难在于 通过连接的两种性质完全不同的金属进行复合。商用热 电偶在非常昂贵的机器上使用电容放电技术进行焊接以 确保均匀性。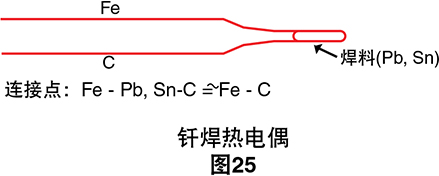
当然,不良焊接会导致连接开路,这可在测量情况下 通过执行热电偶开路检查检测出来。这是数据记录器提 供的一种常见测试功能。尽管热电偶开路是最容易检测 到的故障,但它不一定是最常见的故障模式。
标定降级是一种比热电偶开路严重得多的故障情况, 因为它可能会导致温度读数看起来正确。标定降级描述 无意中更改热电偶线的物理结构以致其在指定的限制内 不再符合NBS多项式的过程。标定降级可导致大气颗粒 扩散到金属中(由极限温度引起)。这可能由高温退火 或冷加工金属导致,即从线管中抽出电线或应变野蛮操 作或振动时产生的影响。退火可能会在经历温度梯度的 电线段内发生。
罗伯特莫法特在他的《Gradient Approach to Thermocouple Thermometry》中解释说,热电偶电压 实际上是由包含温度梯度的电线段生成的,而不一定是 由连接点生成的。9例如,如果有一个热探头位于金属液 槽中,则将有两个几乎等温的区域并且其中一个有较大 的梯度。
在图26中,热电偶连接点将不会产生输出电压的任何 部分。阴影部分是将产生几乎整个热电偶输出电压的部 分。如果发现此热电偶的输出由于老化或退火而出现漂 移,则单独更换热电偶连接点将无法解决该问题。我们 将不得不更换整个阴影部分,因为这是热电偶电压的 来源。
热电偶线显然无法完美制造;会有一些缺陷导致输出 电压误差。这些不均匀性如果出现在急剧变化的温度梯 度区域可能会尤其有破坏性。由于我们不知道电线内部 将会产生缺陷的位置,因为我们能做的是避免产生 急剧变化的梯度。通过使用金属套管或仔细布置热电偶 线可减小梯度。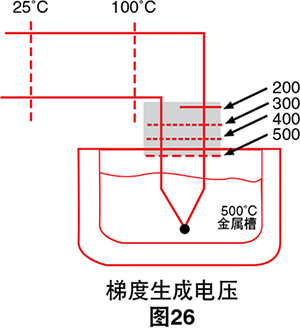
高温可能还会对热电偶线绝缘体造成损害。绝缘电阻 可能会随着温度升高呈指数下降,甚至到产生虚拟连接 点的程度。7假设我们在高温下运行完全开路的热电偶
泄漏电阻RL可能足够低以形成完整的电路,并为我们 提供一个不正确的电压读数。现在,我们假设热电偶并 非开路,但我们使用的是一段很长的小直径电线。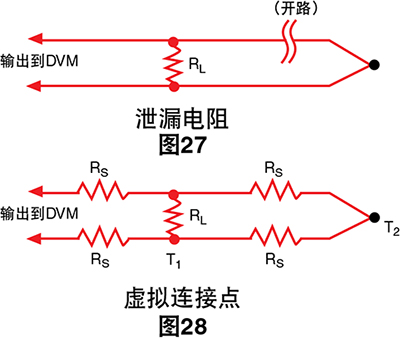
如果热电偶线很小,则其串联电阻RS将相当高并且在 极端条件下RL < < RS。这意味着热电偶连接点将显示为 位于RL并且输出将与T1而不是T2成正比。
高温会对热电偶线有其他不利影响。绝缘层内的杂质 和化学品可能会实际上扩散到热电偶金属中,导致温度- 电压依赖性偏离公布的值。在高温下使用热电偶时,应 仔细选择绝缘层。通过选择适当的保护性金属或陶瓷护 套,可将大气效应降至最低。
某些热电偶绝缘层中使用的染料在存在水的情况下将 形成电解质。这将产生电蚀作用,得到的输出比塞贝克 效应大几百倍。应采取预防措施以屏蔽热电偶线避免所 有恶劣的大气和液体环境。
制成的热电偶不能没有质量。由于加热任何质量都需 要能量,因此热电偶将稍微改变其打算测量的温度。如 果要测量的质量较小,则热电偶自然必定很小。但使用 小直径电线制成的热电偶更容易受到污染、退火、应变 和并联阻抗等问题的影响。要最大限度降低这些影响, 可以使用热电偶延长线。市售的延长线主要用于覆盖测 量热电偶和电压表之间的长距离。
延长线由塞贝克系数与特定热电偶类型非常相似的金 属制成。通常它的尺寸更大以便其串联电阻不会在横跨 长距离时成为影响因素。它还可以比非常小的热电偶线 更容易穿过线管。延长线指定的温度范围通常比优质热 电偶线低得多。除了提供实用的尺寸优势以外,延长线 还比标准热电偶线便宜。这对基于铂的热电偶来说尤其 实际。
由于延长线指定的温度范围较窄并且很可能会受到机 械应力,因此延长线的温度梯度应保持在最低限度。根 据梯度理论,这可确保几乎没有任何输出信号受延长线 影响。
噪声-我们已经讨论了线路相关的噪声,因为它与数据 采集系统有关。积分、树形开关和保护技术可用于抵消 大多数线路相关的干扰。宽带噪声可通过模拟滤波器 抑制。
数据采集系统无法抑制的一种噪声类型是由系统中的 直流泄漏电流导致的直流偏移量。尽管直流泄漏电流量 值足以导致显著误差的情况不常见,但应注意并防止其 出现的可能性,尤其是热电偶线非常小而相关的串联电 阻很高时。
热电偶线按照特定的规格制造,表明其符合NBS表的 标准。规格有时可通过校准电线(在已知的温度进行测 试)来增强。连续线轴上的连续电线件通常会比指定的 公差更接近地跟踪彼此,尽管其输出电压可能稍微远离 绝对规格的中心。
如果是为了提高导线的基本规格而校准导线,更为迫 切的工作是需要具备上述所有条件以避免失准。
记录文档-说记录文档是电压测量误差的来源之一看 起来有些不合适,但实际上,热电偶系统由于易于使用 而引入了大量数据点。海量的数据可能变得相当不易操 作。采用大量数据时,由于标错线、使用错误的NBS曲 线等导致错误的可能性随之增加。
由于通道号不断变化,因此数据应按测量而不仅仅是 通道号进行分类。6有关任何指定测量以及如传感器类 型、输出电压、典型值和位置之类的信息均可在一个数 据文件中进行维护。这可以在计算机控制下完成,也可 以仅仅通过填写预先打印的表格来完成。无论如何维护 数据,都不应低估简明系统的重要性,尤其是在开始复 杂的数据收集项目时。
我们已经提到过的大多数误差来源在其温度限制附近 使用热电偶时会更加严重。在大多数应用中,不会经常 遇到这些情况。但我们在高温、恶劣的大气环境中使用 小型热电偶的情况将会怎样?我们怎么知道热电偶什么 时候产生错误的结果?我们需要制定一套可靠的诊断 步骤。
通过使用诊断技术,R.P.里德已开发出一个优良的系统 用于检测故障热电偶和数据通道。10此系统的三个组件是 事件记录、温区框测试和热电偶电阻历史记录。
事件记录-第一个诊断根本不是测试,而是记录可能甚 至远程影响测量的所有相关事件。示例如下
3月18日事件记录
10:43 电源故障
10:47 系统电源恢复
11:05 将M821改为K型热电阻
13:51 新数据采集程序
16:07 M821似乎出现读数错误
图29
我们查看程序列表并发现被测量#M821使用J型热电偶 并且我们的新数据采集程序将其视为J型。但通过事件记 录,很明显热电偶M821被更改为K型,而该更改未输入 到程序中。虽然大多数异常不会这么容易发现,但事件 记录可为系统测量中不明更改的原因提供有价值的洞察。 这对于配置为测量几百个数据点的系统尤其实际。
温区框测试-温区框是用于代替冰槽基准的已知温度的 等温接线盒。如果我们暂时将热电偶直接在温区框中 短路,则系统应读取非常接近温区框的读数,即接近 室温。
如果热电偶导线电阻比并联电阻高得多,则铜线分流 强制V = 0。在未短路的正常情况下,我们需要测量TJ, 而系统读数为:
V ≅ α (TJ - TREF)
但对于功能测试,我们已使端子短路,以使V=0。因此 指示的温度T’J为:
0 = α (T’J - TREF)
T’J = TREF
因此,对于V = 0的dvm读数,系统将指示温区框温 度。首先我们观察温度T (强制与T 不同),然后 我们缩短铜线热电偶,并确保系统指示温区框温度而 不是TJ。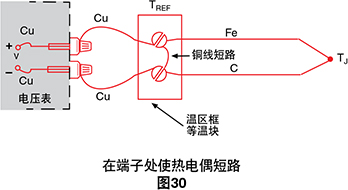
这一简单的测试确认控制器、扫描器、电压表和温区框 补偿都正常运行。实际上,这一简单的过程可测试除热 电偶线本身以外的所有内容。
热电偶电阻-热电偶电路电阻的急剧变化可作为警告指 示器。如果绘制每组热电偶线的电阻与时间曲线,我们 可以立即发现急剧电阻变化,这可能表示电线开路、由 于安装故障电线短路、由于振动疲劳发生变化或许多故 障机制之一。
例如,假设我们有如图31中所示的热电偶测量。 我们想要测量已经点燃的地下煤层的温度曲线。电线
经过高温区域,然后进入冷却器区域。我们测量的温度
突然从300˚C上升到1200˚C。是煤层的燃烧区域转移到 不同的位置,还是热电偶绝缘层发生故障,因而导致热 点的两根电线之间短路? 示例如下: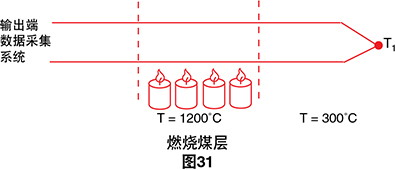
如果我们拥有热电偶线电阻的连续历史记录,则可以 推断出实际发生的事情。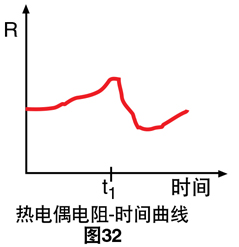
由于电线的电阻率随着温度变化而变化,因此热电偶 的电阻自然随时间变化。但电阻的突然变化表示有些错 误。在这种情况下,电阻会急剧下降,表示绝缘层发生 故障,有效地缩短了热电偶回路。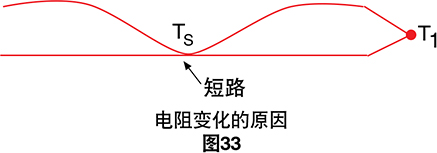
连接点将测量温度Ts而不是T1。电阻测量为我们提供了 更多信息,有助于解释标准热电偶开路检查检测到的物 理现象。
测量电阻-我们大概检查一下热电偶线的电阻,如同进 行一次简单的测量。但要记住,如果热电偶产生电压, 这个电压可能会导致大的电偶测量误差。测量热电偶的 电阻类似于测量电池的内部电阻。我们可以使用称为偏 置补偿欧姆测量的技术来解决这个问题。
顾名思义,电压表首先测量热电偶偏移电压而不应用 欧姆电流源。然后,欧姆电流源将打开并再次测量电阻 两端的电压。电压表软件会补偿热电偶的偏移电压并计 算实际的热电偶源电阻。
特殊热电偶-在极端条件下,我们甚至可以使用诊断热 电偶电路配置。尖端分支和管脚分支的热电偶是四线热 电偶电路,可以进行温度、噪声、电压和电阻的冗余测 量以检查线路完整性。其各自的优点在参考资料8中详细 讨论。
只有严苛的热电偶应用才需要如此大量的诊断,但令 人欣慰的是,知道存在可用于确认重要热电偶测量完整 性的过程。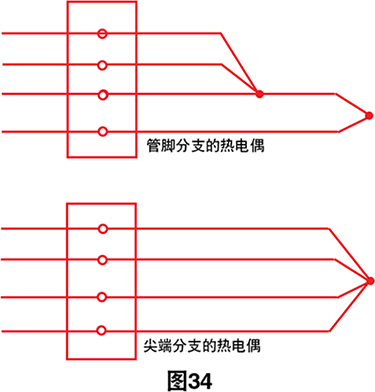
总之,可通过以下预防措施改善热电偶系统的完整性
- 使用不会从测量表面分流掉热量的可能的最大线 径导的线。
- 如果需要小线径线,请仅在测量区域使用,并为 没有温度梯度的区域使用延长线。
- 避免可能会拉紧线的机械应力和振动。
- 使用长热电偶线时,请连接屏蔽dvm保护端子的 线,并使用双绞延长线。
- 避免急剧的温度梯度
- 尝试恰好在热电偶线的额定温度时使用该热电 偶线。
- 使用防护型积分模数转换器。
- 在恶劣的环境中使用适当的护套材料来保护热 电偶线
- 仅在温度低且梯度小的区域内使用延长线。
- 保留热电偶电阻的事件记录和连续记录。
塞贝克发现热电现象的同一年,汉弗莱戴维爵士宣 布,金属的电阻率表现出明显的温度依赖性。五十年
后,威廉西门子爵士提出使用铂作为电阻温度计中的元 件。他的选择被证明是最合适的,正如铂如今用作所有 高精度电阻温度计中的主要元件。实际上,铂电阻式温 度检测器15(或PRTD)如今被用作从氧点(-182.96˚C) 到锑点(630.74˚C)的内插标准。
铂尤其适合此目的,因为它能够在承受高温同时保持 出色的稳定性。作为一种贵金属,它表现出对污染有限 的敏感度。
使用铂的经典电阻式温度检测器(RTD)结构由C.H.梅 尔斯于1932年提出。12他将一个铂螺旋线圈缠在一个交 叉的云母圈上并在一个玻璃管内安装该组件。此结构将 电线上的应力减至最低,同时使电阻升至最高。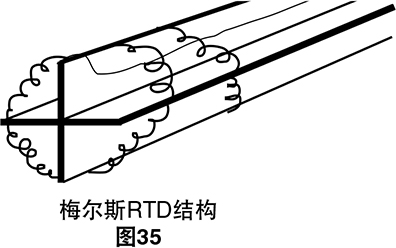
尽管此结构可以产生非常稳定的元件,但铂和测量点 之间的热接触相当差。这会导致热响应速度较慢。该结 构的脆弱限制了如今将其主要用作实验室标准。
另一项实验室标准取代了梅尔斯的设计。此设计是埃 文斯和伯恩斯提出的鸟笼元件。16铂元件保持大部分不 受支撑,这使得它可以在因温度变化膨胀或收缩时自由 移动。
应力诱导的电阻随时间变化并且温度因此降至最低, 而鸟笼成为最终的实验室标准。由于不支持的结构和随 后的振动敏感度,此配置对于工业环境来说仍然有些太 脆弱了。
更坚固的制造技术如图37中所示。双股铂线缠绕在玻 璃或陶瓷线轴上。双线绕组减小了线圈的有效封闭区 域,从而将电磁效应及其相关噪声减至最低。一旦线缠 绕在线轴上后,组件随即使用一层玻璃液密封。密封过 程确保了RTD将在极端振动情况下保持其完整性,但同 时也限制了铂金属在高温下的膨胀。除非铂和线轴的膨 胀系数完全匹配,否则随着温度的变化,电线上会产生 应力,导致应力诱导的电阻变化。这可能导致线电阻的 持久变化。
部分支持版本的RTD可提供鸟笼方法和密封螺旋结构 之间的折衷。其中一种方法是使用铂螺旋结构穿过陶瓷 圆筒并通过玻璃料粘贴。这些设备将在中等严苛的振动 应用中保持出色的稳定性。 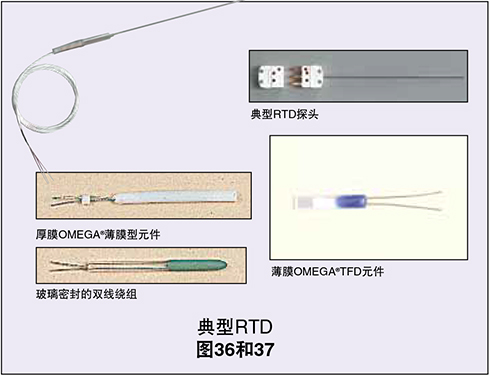
在最新的制造技术中,铂或金属-玻璃浆膜会沉积或 筛选到一个小的扁平陶瓷基体中,使用激光微调系统蚀 刻,然后进行密封。涂膜RTD可大幅减少装配时间,并 且具有可增大指定尺寸设备的电阻这一更大的优势。采 用该制造技术,设备本身的尺寸就可以做到很小,这表 示设备可以更快响应温度的阶跃变化。涂膜RTD不如手 工制造的同类产品稳定,但因其在规模和生产成本上的 决定性优势正变得越来越流行。这些优势会推动将来提 高稳定性所需的研究。
金属-所有金属都会对温度的正变化产生正电阻变化。 这当然就是RTD的主要功能。正如我们很快将看到的 一样,RTD电阻标称值较大时系统误差将被减至最低。 这意味着金属线的电阻率较高。金属的电阻率越低, 我们就必须使用越多的材料。
表6列出了常见RTD材料的电阻率
金属
+
-
|
|
电阻率 OHM/CMF (cmf = 圆密耳英尺) |
|
金
Au
|
|
13.00 |
|
银
Ag
|
|
8.8 |
|
铜
Cu
|
|
9.26 |
|
铂
Pt
|
|
59.00 |
|
钨
w
|
|
30.00 |
|
镍
Ni
|
|
36.00 |
表6 |
由于其较低的电阻率,金银很少用作RTD元件。钨有 着相对较高的电阻率,但它保留用于非常高温度下的应 用,因为它极其脆弱并且难以使用。
铜偶尔会用作RTD元件。其较低的电阻率强制要求元 件比铂元件长,但其线性度和非常低的成本使其成为一种经济的替代品。其温度上限仅为约120˚C。
最常见的RTD由铂、镍或镍合金制成。经济的镍衍生 线可在有限的温度范围内使用。它们相当非线性,并且 往往会随时间出现漂移。铂显然是实现测量完整性的理 想选择。
铂RTD的常用电阻值范围,从鸟笼型RTD的10欧姆到 涂膜RTD的数千欧姆。一个最常用的值是100欧(0˚C)。 铂线的DIN 43760标准温度系数是α = 0.00385。对 于100欧姆的线,这相当于+ 0.385 OHMS/˚C (0˚C)。 α的这个值实际上是从0˚C到100˚C的平均斜率。铂电阻 标准中使用的化学上更纯的铂线的α值是+0.00392欧姆/ 欧姆/˚C。
斜率和绝对值都是较小的数值,尤其是考虑到引至传 感器的测量线可能为几欧姆甚至几十欧姆的事实。较小 的导线阻抗也可能对我们的温度测量造成显著误差。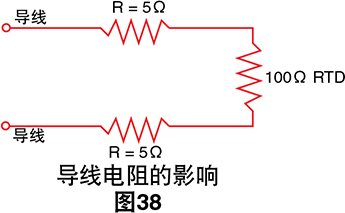
十欧姆的导线阻抗意味着10/0.385 ≅ 26˚C的测量误 差。即使导线的温度系数也可能会造成测量误差。避免 此问题的经典方法是使用电桥。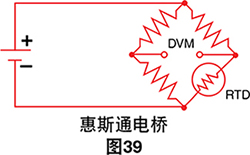
电桥输出电压是RTD电阻的间接指示。电桥需要四根 连接线、一个外部源以及三个零温度系数的电阻。为避 免三个桥接完成的电阻与RTD承受相同的温度,RTD将 通过一对延长线与电桥隔开:
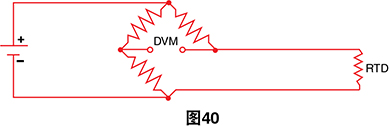
这些延长线会重新产生我们最初遇到的问题:延长线 的阻抗会影响温度读数。这一影响可通过使用三线电桥 配置减至最低: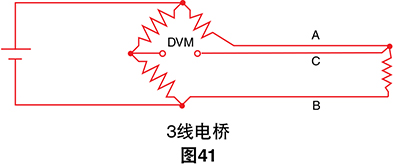
如果线A和B长度完全匹配,则其阻抗影响将抵消,因为 它们位于电桥相反的分支中。第三根线C充当感应导线 并且不带电流。
图41中所示的惠斯通电桥在电阻变化和电桥输出电压 变化之间建立了非线性关系。这需要其他方程来将电桥 输出电压转换为等效的RTD阻抗,合成RTD的已存在非 线性温度-电阻特性。
4线电阻- 使用电流源及远程感应数字电压表的技术可 缓解与电桥有关的许多问题。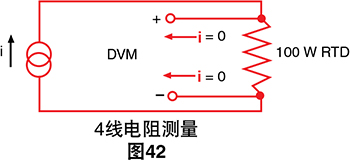
dvm读取的输出电压与RTD电阻成正比,因此只需一个转 换公式。三个桥接完成的电阻被一个基准电阻替换。数字 电压表仅测量RTD两端的压降并且对导线的长度不敏感。
使用4线电阻的一个缺点是我们需要的延长线比3线电 桥多一根。如果我们注重温度测量的精度,这只是很小 的代价 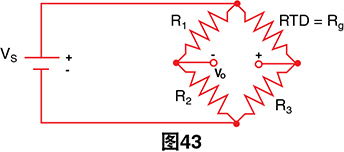
如果我们知道VS和VO,则可以计算出Rg,然后求解 温度。通过R1 = R2构建的电桥的不平衡电压Vo为:
很小 的代价 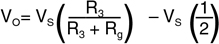
如果Rg = R3,则VO= 0并且电桥实现平衡。这可以手动 完成,但如果我们不想手动进行电桥平衡,可以仅求解 VO形式的Rg:

该表达式假定导线电阻为零。如果Rg的位置离3线配置 中的电桥有一段距离,则导线电阻RL将与Rg和R3串行。
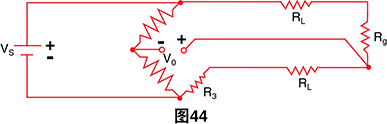
我们再次求解Rg:
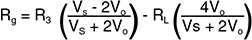
如果Vo较小(即电桥接近平衡),则误差项较小。此 电路与应力表之类的设备可以很好地配合使用,从而只 更改电阻值几个百分点,但RTD电阻随温度显著变化。 假设RTD电阻为200欧姆,而电桥设计用于100欧姆: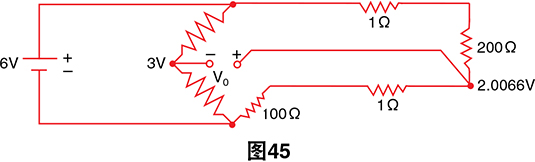
由于我们不知道RL的值,因此必须使用公式(a),所以 得到:
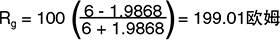
正确的答案当然是200欧姆。即温度误差约为2.5˚C。
除非您能够实际测量RL的电阻或平衡电桥,否则基本 的3线技术并非使用RTD测量绝对温度的精确方法。更 好的方法是使用4线技术。
RTD是比热电偶更线性化的设备,但它仍需要曲线拟 合。Callendar-Van Dusen方程用于粗略估计RTD曲线已 有多年:11, 13
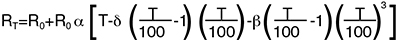
其中:
RT = 温度为T时的电阻
Ro = T = 0˚C时的电阻
α = T = 0˚C时的温度系数
(通常为+0.00392Ω/Ω/˚C)
δ = 1.49(.00392 铂的典型值)
β = 0 T > 0
0. 11(典型值)T < 0
系数α,β和δ的确切值通过在四个温度测试RTD并求解 相关方程确定。为提供更精确的曲线拟合,这个熟悉的 方程在1968年由20次多项式取代。
打印出此方程表明RTD是比热电偶更线性化的设备: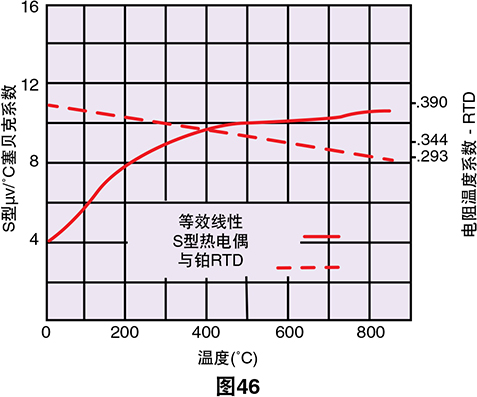
适用于热电偶的实用预防措施同样也适用于RTD,即 使用屏蔽和双绞线、使用适当的护套、避免应力和急剧 变化的梯度、使用尺寸较大的延长线、保留良好的记录 文档和使用保护的积分dvm。此外,应遵从以下预防 措施。
结构-由于其结构,RTD在某种程度上比热电偶更脆 弱,并且必须采取预防措施进行保护。
自动加热-与热电偶不同的是,RTD并非自供电。电流 必须经过设备才能提供可进行测量的电压。电流会导致 RTD内的焦耳(I2R)加热,从而更改其温度。这一自动加 热会导致出现测量误差。因此,必须注意欧姆表提供 的测量电流的量值。自动加热误差的典型值为自由空气 中 1⁄2˚C/毫瓦。显然,浸入导热介质中的RTD会将其焦耳 热量传递给介质,并且由于自动加热导致的误差将因此 减小。在自由空气中上升1˚C/毫瓦的同一RTD在以
1米/秒速率流动的空气中仅上升1⁄10˚C/毫瓦。6
要减小自动加热引起的误差,请使用仍可提供所需分 辨率的最小欧姆测量电流,并使用仍可提供良好响应时 间的最大RTD。显然,这需要考虑折衷。
热分流-热分流是通过插入测量传感器更改测量温度 的行为。热分流对于RTD来说比热电偶问题更大,因为 RTD的物理体积比热电偶大。
小型RTD |
大型RTD |
| 响应迅速 热分流低 自动加热误差高 |
响应缓慢 热分流较差 自动加热误差低 |
热电动势-RTD进行测量时,制成的铂-铜连接可能会导致 热偏移电压。偏移补偿欧姆技术可用于消除这一影响。
与RTD一样,热敏电阻也是温度敏感的电阻。如果说 热电偶是最通用的温度传感器而PRTD是最稳定的,则 最适合描述热敏电阻的词是敏感。在三种主要的传感器 分类中,热敏电阻表现出目前为止最大的随温度参数变 化
热敏电阻通常由半导体材料制成。尽管可以使用正 温度系数装置,但大多数热敏电阻都使用负温度系数 (TC);即其电阻随着温度升高而减小。负T.C.的大小可 以是每摄氏度几个百分点,以便热敏电阻电路能够检测 到温度的微小变化,而使用RTD或热电偶电路无法观察 到这样的变化。
我们为这一灵敏度提高付出的代价是损失线性度。热 敏电阻是一个极端的非线性设备,它高度依赖于工艺参 数。因此,制造商无法将热敏电阻曲线标准化到RTD和 热电偶曲线的标准化程度。
单独的热敏电阻曲线可能非常接近通过使用
Steinhart-Hart 方程取得的近似:18 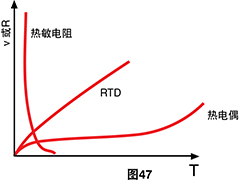
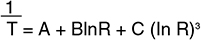
其中:
T = 开氏度
R = 热敏电阻的电阻
A,B,C = 曲线拟合常数
A、B和C通过在公布的数据曲线上选择三个数据点并求 解三个联立方程得出。选择的数据点在热敏电阻温度范 围标称中心内的跨度不超过100˚C时,此方程接近相当 显著的±.02˚C曲线拟合。
通过更简单的方程可以达到更快一些的计算机执行 时间: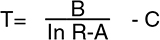
其中A、B和C可通过选择三个(R,T)数据点并求解三个得 到的联立方程再次得出。此方程必须在较窄的温度范围 内应用以便接近Steinhart-Hart方程的精度。
我们投入了大量努力开发接近线性特性的热敏电阻。 这些通常是2或4线设备,需要极度匹配的电阻才能线性 化特性曲线。现代数据采集系统及其计算控制器使这种 硬件线性化不再有必要。
热敏电阻的高电阻率为其提供了独特的测量优势。使 用RTD无需四线电阻测量。例如,常见的热敏电阻值为 5000欧姆(25˚C)。通过典型T.C.的4%/˚C,100欧姆的测 量导线电阻仅产生0.05˚C的误差。这一误差因素比同等 RTD误差小500倍。
缺点-由于是半导体,热敏电阻比RTD或热电偶更容易 在高温下永久失准。热敏电阻的使用通常限于几百摄氏 度并且制造商会发出警告,长时间暴露在即使远低于最 大工作限制的温度下也将导致热敏电阻偏离其指定的 公差。
热敏电阻可制成非常小的尺寸,这意味着它们将快速 响应温度变化。这还意味着其较小的热质量使其特别容 易受自动加热误差的影响。
热敏电阻比RTD或热电偶脆弱得多,并且必须小心安 装以避免破碎或连接分离。
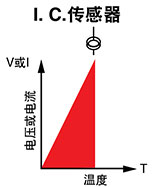
测温法最近的创新是集成电路温度传感器。它在电压 和电流输出配置中均可用。两者均提供与绝对温度成线 性比例的输出。典型值为1 μA/K和10 mV/K。
除了提供与温度非常接近线性的输出以外,这些设备 还共享热敏电阻设备的缺点并因此具有有限的温度范 围。自动加热和脆弱的问题同样很明显,并且它们需要 外部电源。
这些设备提供了一种方便的途径,可以产生与温度成 正比的模拟电压。因此硬件热电偶参比端补偿电路中出 现了这样的需求(见图15)。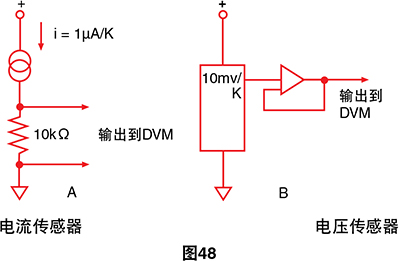
以下示例列出了根据经验得出的热电偶“定律”,对 于理解和诊断热电偶电路很有用。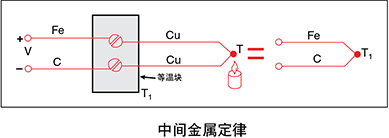
在铁和康铜导线之间插入铜导线将不会改变输出电压 V,无论铜导线的温度如何。电压V是Fe-C热电偶在温度 为T1时的电压。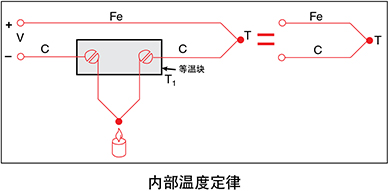
输出电压V将为Fe-C对在温度为T时的电压,不论是否对 任一测量导线应用外部热源。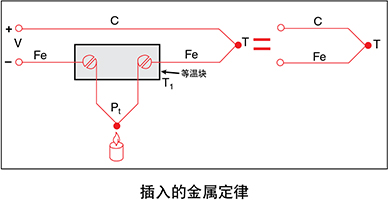
电压V将为Fe-C热电偶在温度为T时的电压,只要铂线 的两端为相同温度。铂线产生的两个热电偶(Fe-Pt和 Pt-Fe)相对作用。
所有上述示例假设测量线是均匀的;即没有缺陷和 杂质。
多年来,我们已开发出特定的热电偶对合金来解决独 特的测量问题。较常见的热电偶特性在此处讨论。
我们将使用的术语标准线误差是指《ASTM标准年鉴》中发布的常见商用规格。它表示实际热电偶输出电压与 NBS专题论文125的表中预测的电压之间允许的偏差。
贵金属热电偶-贵金属热电偶(B型、R型和S型)都是 铂或铂-铑热电偶,因此共享许多相同的特性。
扩散-高温下的金属蒸汽扩散可以轻易改变铂线的校 准;因此,铂线应仅在非金属护套(例如高纯度氧化 铝)内使用。此规则的一个例外是铂制成的护套,但 此选件非常昂贵。
稳定性-基于铂的对是目前所有常见热电偶中最稳定 的。S型如此稳定以致被指定为锑点(630.74˚C)与金点 (1064.43˚C)之间温度校准的标准。
B型-B型对是唯一表现出双值不确定性的常见热电偶。
由于双值曲线和低温下极低的塞贝克系数,B型在低 于50˚C时几乎无效。由于输出接近零(从0˚C到42˚C),因此B型的唯一优点是只要温度介于0˚与40˚C之间,参比端温度几乎无关紧要。当然,测量连接点温度通常 都非常高。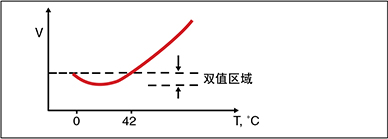
与贵金属热电偶不同,这些基本金属对没有特定的化学 成分。可以使用金属的任意组合,这可产生标准线误差 范围内的电压-温度曲线拟合。并且会带来一些非常有 趣的金属组合。例如康铜,它根本不是一个具体的金属 合金,而是整个铜镍合金系列的通用名称。不可思议的 是,T型(铜-康铜)热电偶中使用的康铜与J型(铁- 康铜)对中使用的康铜是不一样的。3
E型-尽管不指定低于0˚C的E型标准线误差,但E型热电 偶非常适合低温测量,因为它塞贝克系数高(58 μV/˚C)、 导热性低并且耐腐蚀。
E型的塞贝克系数大于所有其他标准对,使其对于检 测较小的温度变化非常有用。
J型-J型对中的正极元件铁是一种便宜的金属,很少以 纯净的形式制造。J型热电偶由于铁中的杂质而一致性 特性较差。即使如此,由于其塞贝克系数高并且价格 低,J型对仍然很受欢迎。
J型对应切勿在超过760˚C时使用,因为突然的磁性 转变可导致即使仪器冷却后仍存在的失准。
T型-这是公布的标准线误差适用于温度区域低于0˚C 的唯一对;但E型实际上更适合非常低的温度,因为其 塞贝克系数较高并且导热性较低。
T型独特的区别在于有一根铜导线。这在温差均为预期 的专门监测情况下可能成为一个优点。
优点是铜热电偶导线与dvm端子是同一种金属,因此 不必进行导线补偿。
K型与镍铬硅电偶合金 - 镍铬硅热电偶(即N型)与 K型类似,但设计为将传统镍铬-镍铝组合中的某些不稳 定性减至最低。合金含量的变化提高了500˚C时发生的 有序/无序变化,正极元件中更高的硅含量提高了高温下 的耐氧化性。特性曲线的完整说明在NBS专题论文161 中发布。14
钨-钨-铼热电偶通常在高温的缺氧或真空环境中使用, 但由于高反应率而从不在氧化气体中使用。纯钨在加热 超过其再结晶温度(约1200˚C)时会变得非常脆弱。为 使导线更容易操作,在两个热电偶分支中都使用了铼合 金。G型(钨与含铼26%的钨铼合金)、C型(含铼5% 的钨铼合金与含铼26%的钨铼合金)和D型(含铼3%的 钨铼合金与含铼25%的钨铼合金)热电偶可作为裸线形 式以及完整的探头组件提供。所有材料都符合公布的误 差限。
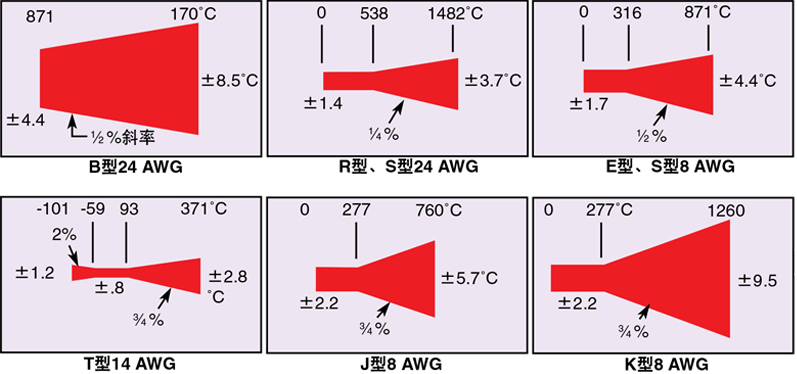
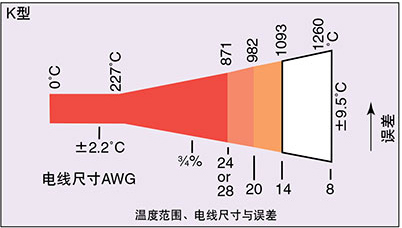
在高温下,尺寸较小的 热电偶线受扩散、杂质 和不均匀性的影响比大 尺寸线大得多。标准线 误差体现了这一关系。请注意,每种NBS线误 差规格都带有电线尺寸。贵金属热电偶(B、R和S)明显 出于成本原因指定为小尺寸(24 ga.)线
|
DIA, MILS |
DIA, mm |
| 8 |
128 |
3.3 |
| 10; |
102 |
2.6 |
| 12 |
81 |
2.1 |
| 14 |
64 |
1.6 |
| 16 |
51 |
1.3 |
| 18 |
40 |
1 |
| 20 |
32 |
0.8 |
| 22 |
25 |
0.6 |
| 24 |
20 |
0.5 |
| 26 |
16 |
0.4 |
| 28 |
13 |
0.3 |
| 型号 |
金属
+
-
|
J标准色码
+
-
|
两英尺
20 AWG |
塞贝克系数S
( V/˚C) @ T (˚C) |
˚C标准线误差
(见附录B) |
NBS指定的材料范围†
(˚C) |
| B |
含铑6%的铂铑合金
含铑30%的铂铑合金
|
– |
0.2 |
6
600
|
4.4到8.6 |
0到1820* |
| E |
含铬10%的 镍铬合金
康铜
|
紫
红色
|
0.71 |
58.5
0
|
1.7到4.4 |
-270到1000 |
| J |
铁
康铜
|
白色
红色
|
0.36 |
50.2
0
|
1.1到2.9 |
-210到760 |
| K |
含铬10%的镍铬合金
镍
|
黄色
红色
|
0.59 |
39.4
0
|
1.1到2.9 |
-270到1372 |
| N (AWG 14) |
镍铬硅合金
镍硅合金
|
– |
– |
39
600
|
– |
0到1300 |
| N (AWG28) |
镍铬硅合金
镍硅合金
|
– |
– |
26.2
0
|
– |
-270到400 |
| R |
含铑13%的铂铑合金
铂
|
– |
0.19 |
11.5
600
|
1.4到3.8 |
-50到1768 |
| S |
含铑10%的铂铑合金
铂
|
– |
0.19 |
10.3
600
|
1.4到3.8 |
-50到1768 |
| T |
铜
康铜
|
蓝色
红色
|
0.30 |
38
0
|
0.8到2.9 |
-270到400 |
| W-Re |
含铼5%的钨铼合金
含铼26%的钨铼合金
|
– |
– |
19.5
600
|
– |
0到2320 |
* B型双值低于42˚C - 指定的曲线拟合仅在130˚C以上
† 材料范围适用于8 AWG线;随着电线尺寸减小而缩小
|

参考文献
|
| 1 |
Charles Herzfeld, F.G. Brickwedde: Temperature - Its Measurement and Control in Science and Industry, Vol. 3, Part 1,Reinhold, New York, 1962. |
| 2 |
Robert P. Benedict: Fundamentals of Temperature, Pressure and Flow Measurements, John Wiley & Sons, Inc., New York, 1969. |
| 3 |
Manual on the Use of Thermocouples in Temperature Measuremen ASTM Special Publication 470A, Omega Press, Stamford, Connecticut 06907, 1974. |
| 4 |
Thermocouple Reference Tables, NBS Monograph 125, National Bureau of Standards, Washington, D.C., 1979. Also, Temperature- Millivolt Reference Tables-Section T, Omega Temperature Measurement Handbook, Omega Press, Stamford Conne 06907,1983. |
| 5 |
H. Dean Baker, E.A. Ryder, N.H. Baker: Temperature Measuremen Engineering, Omega Press, Stamford, Connecticut 06907, 1953. |
| 6 |
Temperature Measurement Handbook, Omega Engineering, Inc., Stamford, Connecticut. |
| 7 |
R.L. Anderson: Accuracy of Small Diameter Sheathed Thermocouples for the Core Flow Test Loop, Oak Ridge National Laboratories, ORNL-54011 (available from National Information Service), April, 1979. |
| 8 |
R. R Reed: Branched Thermocouple Circuits in Underground Coal Gasification Experiments, Proceedings of the 22nd ISA Internationa Instrumentation Symposium, Instrument Society of America, 1976. |
| 9 |
R.J. Moffat: The Gradient Approach to Thermocouple Circuitry, from Temperature - Its Measurement and Control in Science and Industry Reinhold, New York, 1962 |
| 10 |
R.P. Reed: A Diagnostics-Oriented System for Thermocouple Thermometry, Proceedings of 24th ISA International Instrumentation Symposium, Instrument Society of America, 1978. |
| 11 |
Harry R. Norton: Handbook of Transducers for Electronic Measuring Systems, Prentice-Hall, Englewood Cliffs, New Jersey. |
| 12 |
C.H. Meyers: Coiled Filament Resistance Thermometers, NBS Journal of Research, Vol. 9, 1932. |
| 13 |
Bulletin 9612, Rev. B: Platinum Resistance Temperature Sensors, Rosemount Engineering Co., 1962. |
| 14 |
Burley, Powell, Burns & Scroger: The Nicrosil vs. Nisil Thermocoupl Properties and Thermoelectric Reference Data, NBS Monograph 16 U.S. Dept. of Commerce, Washington, D.C., 1978
|
| 15 |
J.P Tavener: Platinum Resistance Temperature Detectors - State of Art, Measurements & Control, Measurements & Data Corporation, Pittsburgh, PA., April, 1974. |
| 16 |
J.P. Evans and G.W. Burns: A Study of Stability of High Temperatur Platinum Resistance Thermometers, in Temperature - Its Measurem and Control in Science and Industry, Reinhold, New York, 1962. |
| 17 |
D.D. Pollock: The Theory and Properties of Thermocouple Elements ASTM STP 492, Omega Press, Stamford, Connecticut 06907, 1979 |
| 18 |
YSI Precision Thermistors, Yellow Springs Instruments, Yellow Spri |
符合ITS- 90标准的热电偶数据在“ITS-90
ouple Direct and Inverse Polynomials”中提供。 |
OMEGA衷心感谢Agilent Technologies允许我们转载《应用 说明290-实用温度测量》。
版权所有© 1997, 2000 Agilent Technologies, Inc. 经许可转载
|
|
|
|